Keywords of Our Research

Our research is in process systems engineering as a subdiscipline of chemical engineering, which also has rich intersections and implications within a broad engineering community. Its methodology is based on applied mathematics, and its application is wide.

The scope of our research, which is computational in nature, can be summarized in five keywords:

Data, Information, Systems, Control, and Optimization.

As many people do, our research group also has an acronym -- DISCO.

DATA & INFORMATION

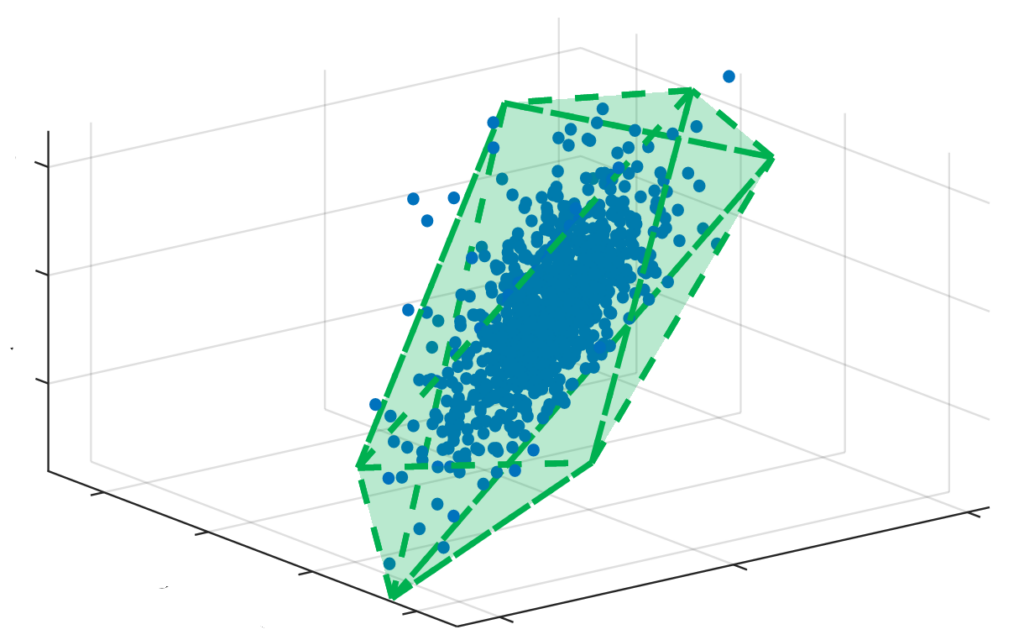
Voluminous records collected from the history as well as simulations provide new approaches to handle complex problems. Built on a probabilistic perspective, statistical and machine learning (ML) algorithms enable flexible data-based characterization and reduce the complexities. This brings complementary strength to engineering research.

We aim at bridging the gap between chemical engineering and the rapidly data science to apply data analytics to a variety of chemical engineering problems. Key to this effort is the understanding of the relation between the engineering first principles (physical laws and experience-based a priori beliefs) and the information contained in empirical observations.

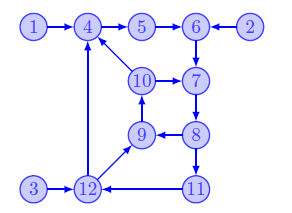
We are in particular interested in studying the methodology for unveiling the underlying structures in obscurity, thereby extracting the essential information needed for high-quality and computational efficient engineering actions.

We are also interested in building digital twins that reflect the physical reality and interact with the actual processes as cyber-physical systems.

SYSTEMS

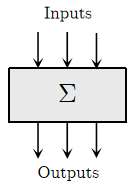
System is a fundamental concept in engineering science, which refers to the quantitative relations between its inputs and outputs as well as the structural patterns underlying these relations. Systems approaches apply to not only classical chemical plants, but also to virtually any engineering systems, including advanced manufacturing, energy systems, logistics and transportation networks, infrastructure, health care, biological systems, and societal systems, etc.

Chemical engineers are often interested in systems with large scales, nonlinearity, uncertainty, as well as other types of complexity that makes it challenging to analyze mathematically. Such a system-level subfield of studies in chemical engineering is often called "process systems engineering" (PSE). With the ongoing development of applied mathematics, systems engineers are increasingly equipped with new perspectives and are developing innovative methodology to encounter the challenges.


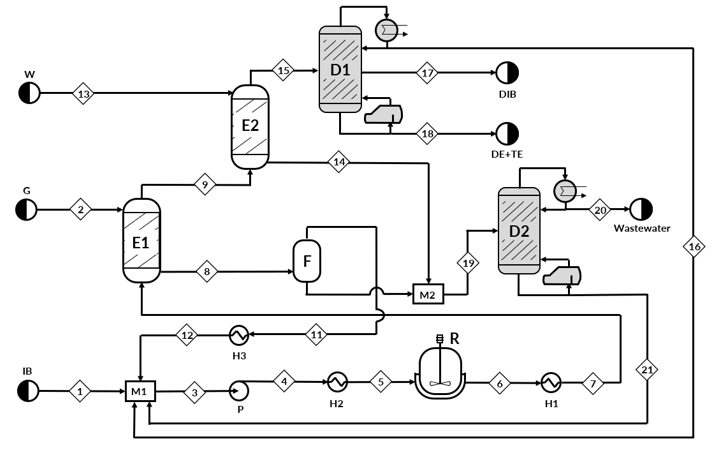
Process Systems Engineering research has become such a fundamental part of industrial automation and control systems that its results have often been integrated into larger industrial solutions and systems.
Many optimization and simulation tools today globally used are de facto results of process system engineering research.
This is not at all a coincidence, since process system engineering has from its very early stages had both a strong focus on industrial problems, as well as, a strong interest from industrial practitioners.

Grossmann & Harjunkoski (2019). Process systems engineering: Academic and industrial perspectives. Computers & Chemical Engineering, 126, 474—484.

CONTROL

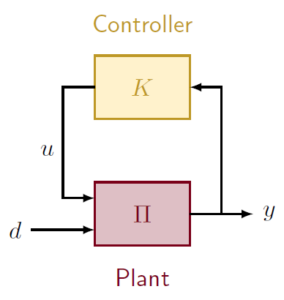
Real-world engineering systems are dynamic. Their states change with time, subject to disturbances, noises and time-varying targets. In order to automate the systems to run around desired setpoints or trajectories, controllers are needed to stabilize and maintain the performance of systems. We leverage nonlinear control theory for the analysis of dynamical systems, especially large-scale ones that arise from typical chemical processes.

The interplay between control theory and optimization and machine learning is evidently of fundamental significance to engineering. We are particularly interested in developing data-driven control frameworks and algorithms that are not only fundamentally innovative but also practically implementable as future-generation process automation technology.

OPTIMIZATION

Engineers are interested in designing and operating safe, sustainable and economically favorable systems. Optimization is the most natural and powerful weapon to tackle these decision making problems. It is also the key ingredient that enables statistical and machine learning from data.

Optimization problems are formulated in the language of mathematical programming, where objective functions are optimized over continuous and integer variables under constraints. We aim to develop efficient and well-performing algorithms for complex optimization problems with diverse forms and structures that are relevant to a multitude of engineering applications.